Qué es el número áureo y cómo afecta a la naturaleza

En el vasto y complejo tejido de la naturaleza, hay patrones matemáticos que se revelan de maneras asombrosas. Uno de estos patrones es el número áureo, también conocido como la proporción áurea o la divina proporción. Representado por el símbolo griego φ (phi), este número, aproximadamente 1.618, tiene profundas conexiones matemáticas y geométricas en el mundo natural. A lo largo de la historia, desde los antiguos egipcios hasta los estudios contemporáneos, se ha observado que el número áureo influye en diversos aspectos de la naturaleza. En este artículo, analizaremos qué es el número áureo y cómo se manifiesta en el reino vegetal, animal, y más allá.

Historia y definición del número áureo

El número áureo, con su representación matemática 1.618, ha llamado la atención de mentes brillantes a lo largo de la historia. Conocido también como la razón áurea, este número irracional surge de una fascinante propiedad geométrica. Al dividir una línea en dos partes de manera que la relación entre la longitud total (a + b) y la longitud de la parte más larga (a) sea igual a la relación entre la parte más larga (a) y la parte más corta (b), se obtiene la proporción áurea. Esta relación se expresa matemáticamente como (a + b) / a = a / b.

La historia del número áureo se remonta a la antigua Grecia, donde matemáticos como Euclides lo exploraron en detalle. Sin embargo, su verdadero reconocimiento y nombre provienen de la obra del matemático italiano Leonardo Fibonacci en el siglo XIII. La conexión entre el número áureo y la secuencia de Fibonacci, donde cada número es la suma de los dos anteriores, agrega otra capa de misterio matemático a esta historia.

Esta proporción también ha trascendido las fronteras de las matemáticas, influyendo en el arte, la arquitectura y la naturaleza misma. Desde la arquitectura de los antiguos egipcios hasta la disposición de pétalos en flores y la formación de galaxias espirales en el cosmos, el número áureo se manifiesta como un elemento intrínseco de la armonía y la proporción en el universo. La ecuación cuadrática x^2 = x + 1, con su solución positiva φ, encapsula la magia matemática que ha cautivado a generaciones a lo largo de los siglos.

Euclides, un antiguo matemático griego, no solo contribuyó significativamente a la geometría, sino que también exploró la relación entre el número áureo y la proporción áurea.

La secuencia de Fibonacci y la conexión con el número áureo

La secuencia de Fibonacci, con su intrigante progresión numérica, desempeña un papel fundamental en la manifestación del número áureo en la naturaleza. Cada número en la secuencia es la suma de los dos anteriores, generando una serie que comienza con 0 y 1, y continúa infinitamente (0, 1, 1, 2, 3, 5, 8, 13, 21, 34, ...). Lo fascinante es que a medida que avanzamos en la secuencia, la proporción entre dos números consecutivos se aproxima constantemente al número áureo, φ (aproximadamente 1.618).

Esta conexión entre la secuencia de Fibonacci y el número áureo no es simplemente una coincidencia matemática, sino un fenómeno profundamente arraigado en la naturaleza. Ejemplos notables incluyen la disposición de las escamas en las piñas de los pinos, los girasoles con sus espirales de semillas, y las conchas de caracol que siguen patrones basados en esta secuencia.

La presencia del número áureo en la secuencia de Fibonacci revela una armonía matemática que se manifiesta en la estructura misma de la vida. Esta relación proporciona una perspectiva intrigante sobre cómo las leyes matemáticas fundamentales pueden permear todos los aspectos de nuestro entorno, desde la más diminuta flor hasta la expansión cósmica de las galaxias.

Sin ir más lejos, la naturaleza muestra una predilección por el número áureo en la disposición de hojas y pétalos. Aunque no todas las plantas siguen este patrón, muchas exhiben espirales logarítmicas que se generan mediante el crecimiento en ángulos no repetitivos, proporcionando una exposición óptima a la luz solar. Este fenómeno se explica mediante instrucciones matemáticas simples, como «crecer primero, luego girar un cierto ángulo y crecer nuevamente». Dichas instrucciones generan patrones repetitivos que culminan en espirales logarítmicas, cuya forma general es la de una espiral áurea.

Leonardo de Pisa, conocido como Fibonacci, iluminó la historia con su genialidad matemática, revelando la aritmética divina que subyace en la secuencia que lleva su nombre.

El número áureo en los animales

El reino animal, fascinante por su diversidad, revela de manera asombrosa la presencia del número áureo en sus estructuras y patrones. Esta proporción matemática, también conocida como la razón áurea, se manifiesta en la disposición de elementos biológicos, desde la más diminuta semilla hasta la complejidad de la anatomía humana.

La disposición de semillas en girasoles proporciona un ejemplo destacado de la influencia del número áureo en la naturaleza. Las espirales concéntricas de semillas siguen patrones basados en la secuencia de Fibonacci, acercándose a la proporción áurea a medida que se expanden. En conchas de nautilus, esta espiral perfecta se forma mediante un crecimiento que se ajusta a la proporción áurea, proporcionando no solo un hogar protector sino también un testimonio visual de las leyes matemáticas subyacentes en la creación.

Incluso en la anatomía humana, la presencia del número áureo es evidente. La relación entre la altura del cuerpo desde el ombligo hasta el suelo y la distancia desde la parte superior de la cabeza hasta el ombligo sigue esta proporción, agregando otra razón matemática a la complejidad biológica.

En síntesis, el número áureo trasciende las fronteras entre lo matemático y lo biológico, revelando una conexión intrínseca en la forma en que la naturaleza organiza sus elementos. Desde las plantas hasta los animales, esta proporción armoniosa parece ser un lenguaje común que se expresa a través de la vida en sus diversas formas y estructuras.

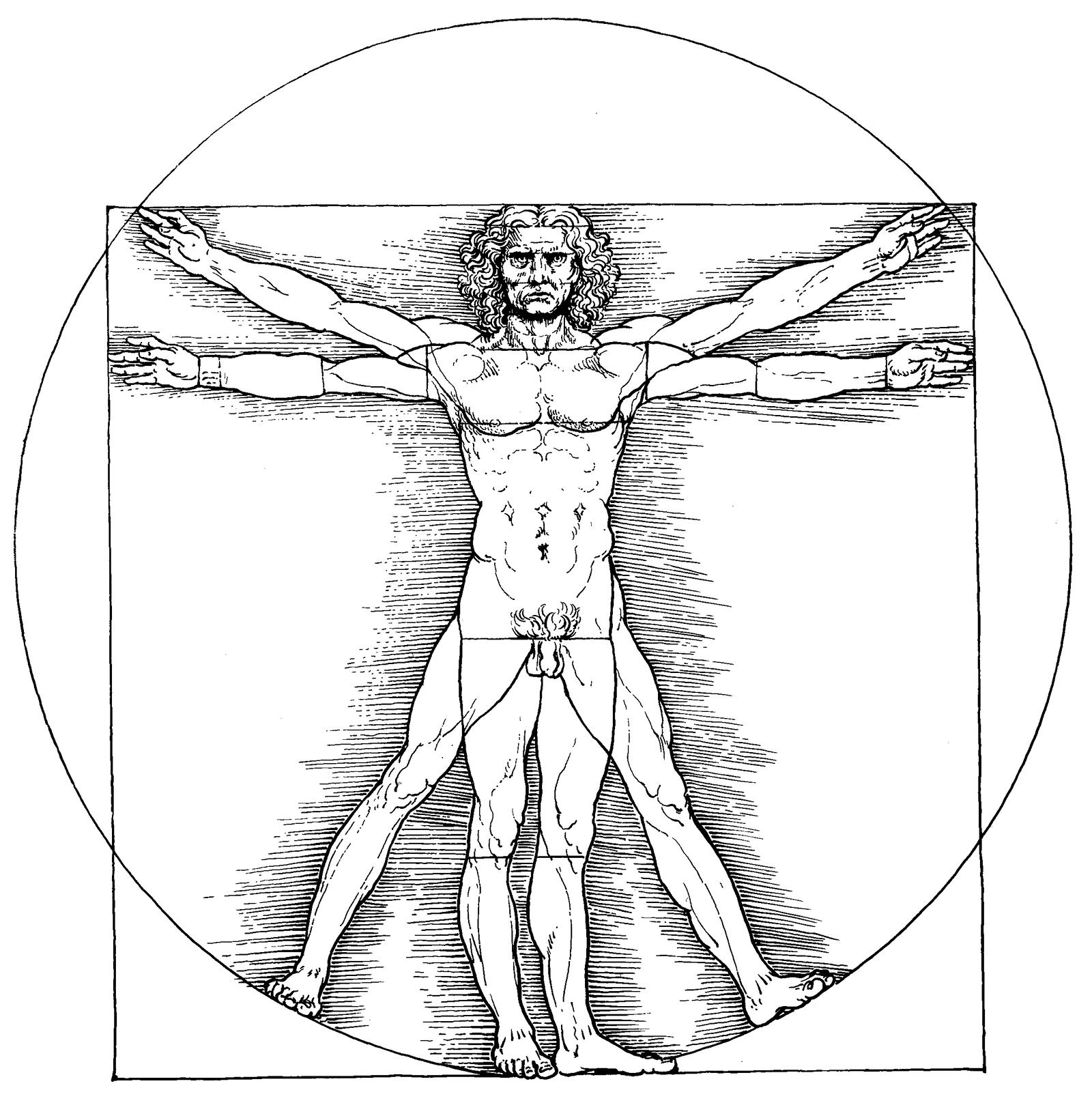
La relación entre el «Hombre de Vitruvio» y el número áureo está relacionada con la búsqueda de proporciones estéticas y armónicas en el arte y la arquitectura.

Ejemplos de la proporción áurea en la naturaleza

La presencia del número áureo en la naturaleza es innegable y abarca una amplia gama de estructuras, desde lo microscópico hasta lo cósmico. En el reino vegetal, la disposición de pétalos en flores revela una armonía matemática. Ejemplos notables incluyen el lirio con tres pétalos, las corolas con cinco, la achicoria con 21, y la margarita con 34, todos siguiendo la secuencia de Fibonacci y aproximándose a la proporción áurea.

La formación de cabezas de semillas también obedece a esta proporción en la naturaleza. En el centro de la cabeza de una flor, las semillas migran hacia el exterior en un patrón espiral, llenando todo el espacio disponible de manera eficiente y armoniosa.

Estructuras como las piñas, el brócoli romanesco y las coliflores siguen el proceso de la secuencia de Fibonacci, demostrando que el número áureo no solo se manifiesta en la disposición de elementos, sino también en el crecimiento y desarrollo de estas estructuras.

Incluso en el mundo arbóreo, las ramas siguen patrones basados en la proporción áurea. El tronco crece hasta que produce una rama, creando dos puntos de crecimiento. Luego, una de las nuevas ramas se divide en dos, dejando la otra inactiva. Este proceso sigue las pautas de la secuencia de Fibonacci, generando una arquitectura de árbol que refleja la armonía matemática en la naturaleza.

Además, fenómenos cósmicos como las galaxias espirales revelan la presencia del número áureo en escalas astronómicas. La disposición de los brazos espirales de la Vía Láctea sigue la forma de una espiral logarítmica, aproximándose a la proporción áurea.

La conexión con el número áureo en el brócoli romanesco es notable debido a su patrón fractal, que exhibe una estructura en espiral que puede aproximarse a las proporciones del número áureo.