En nuestro día a día podemos como comprobar cómo la vida es impredecible. Y es que, como podemos leer, a lo largo del día existen billones de factores que pueden tener un gran impacto en nosotros y en el resto de mundo, pero que nos pasan desapercibidos. Debido a ello, el resultado al final del día puede cambiar por cualquier factor no previsto.

Aún así, los científicos han tratado de identificar las reglas que rigen muchos fenómenos de la naturaleza para permitirnos predecir su evolución, como por ejemplo, el movimiento de los péndulos, de los planetas en órbita, las naves espaciales enviadas, etc. Pero estos unos pocos fenómenos, existiendo otros como la evolución del clima o el flujo de la sangre a través del corazón que parecen imposibles de predecir.

Durante siglos, debido a la complejidad y la multitud de variables en esos fenómenos, se consideraban que eran aleatorios. Ahora sabemos que no lo son, sino que no se disponía de las matemáticas necesarias para entender los patrones hasta que surgió la teoría del caos.

Uno de los creadores de esta nueva teoría fue Henri Poincaré (29 de abril de 1854–17 de julio de 1912), un matemático francés que hizo importantes contribuciones en diversos campos, entre ellos los sistemas dinámicos y la topología.

En 1887, el rey Oscar II de Noruega y Suecia, que había estudiado matemáticas, convoca un concurso de problemas con motivo de su cumpleaños. Poincaré se inscribió. Uno de los problemas era describir la posición de los planetas en el sistema solar en cada momento pasado y futuro siguiendo las ecuaciones de Newton. Y Poincaré pudo identificar la impredecibilidad del sistema, y a pesar de no dar una solución, ganó el premio indicando:

Puede suceder que pequeñas diferencias en las condiciones iniciales produzcan cambios grandes en los fenómenos finales. Un pequeño error producirá un fallo enorme. La predicción se vuelve imposible.

Lorenz y su efecto mariposa

Después de Poincaré, el estudio de los sistemas dinámicos fue bastante olvidado. Así, en la década de 1960, el matemático y meteorólogo Edward Norton Lorenz (23 de mayo de 1917–16 de abril de 2008) se encontró con ese fenómeno al estudiar el clima mediante un modelo matemático de corrientes de aire en la atmósfera.

Un día, quiso repetir una de las simulaciones, pero no partió de los mismos datos que antes, sino que puso como datos de partida unos datos intermedios como resultado de los anteriores cálculos. El resultado fue totalmente distinto.

El ordenador empleaba seis decimales durante los cálculos, pero redondeaba a tres el resultado que ofrecía impreso, que fue el que usó Lorenz. La diferencia entre el dato con tres o seis decimales es menor a 0,0001, por lo que los resultados de la segunda ejecución deberían haber sido muy parecidos a los de la primera. En cambio, las dos evoluciones climáticas predichas por el modelo tomaron caminos completamente separados. De esta forma, Lorenz llegó a la misma conclusión que Poincaré:

Las propiedades del sistema hacían que pequeños cambios en las condiciones iniciales provocaran resultados significativamente diferentes.

Estas observaciones fueron el origen de su famosa charla “Predecibilidad: ¿Puede un aleteo de una mariposa en Brasil desencadenar un tornado en Texas?“. Así, a partir de esa conferencia Lorenz introdujo el término “efecto mariposa”.

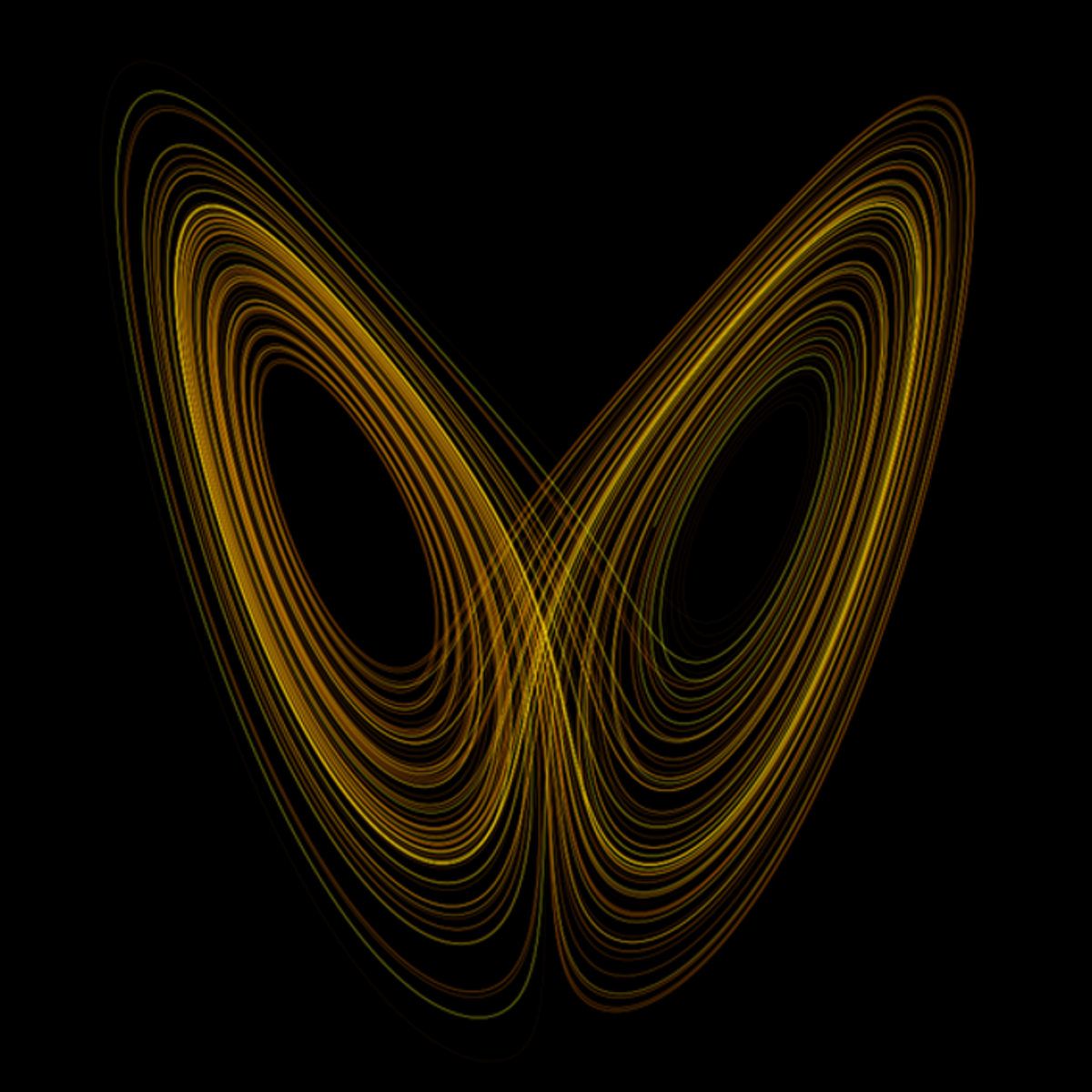
Un icono de la teoría del caos, el atractor de Lorenz. Fuente: Wikimedia

Posteriormente, Stephen Smale (catedrático de la Universidad de California (Berkeley) y reconocido con la medalla Fields en 1966) ideó la llamada herradura de Smale. Con ello, Smale trata de reducir el caos a su expresión fundamental. Esta herradura se trata de una transformación geométrica que al actuar sobre un cuadrado contrayéndolo, dilatándolo y doblándolo lo convierte en una herradura. En base es sencillo, pero cuando se aplica de manera sucesiva acaba llevando a situación caóticas. Un fenómeno que puede aplicarse a casi cualquier aspecto.

¿Como algo ordenado pasa al caos?

Durante la década de 1970, Michell Feigenbaum, descubrió una manera fundamental de explicar cómo se pasa del orden al caos. Usando la potencia de la computación, demostró que existía una constante que aparece en muchas funciones matemáticas antes del inicio del caos. Se trata de un número, alrededor del 4,6692 y que se conoce como la constante de Feigenbaum.

En la década de 1980, el caos estaba de moda. Muchas universidades y centros de investigación crearon grupos de estudio de dinámicas no lineales y sistemas complejos. Así, se popularizaron términos como bifurcación (cuando un pequeño cambio sobre los valores de un sistema provoca un cambio cualitativo repentido en su comportamiento), fractal (imagen del caos) o efecto mariposa. Y la teoría del caos se utilizó para uno de los estudios más populares, como son los fenómenos meteológicos.

La teoría del caos se convirtió en una herramienta matemática perfecta para obtener estructuras ordenadas de un total caos. Se basa en dos ideas principales:

• La primera. Incluso los sistemas mas complejos tienen un orden subyacente.
• La segunda. En esos sistemas, las pequeñas diferencias en las condiciones iniciales (como, por ejemplo, pequeñas variaciones de temperatura) producen resultados muy diferentes, por lo que la predicción de su comportamiento a largo plazo sea imposible.

En otras palabras, la naturaleza determinista de esos sistemas no los hace predecibles, aunque, gracias a la teoría del caos, por lo menos podemos conocer su imprevisibilidad.